Por Julio Batista
Por Sam Baron
Publicado no The Conversation
Muitas pessoas pensam que a matemática é uma invenção humana. Para essa forma de pensar, a matemática é como uma linguagem: ela pode descrever coisas reais no mundo, mas não “existe” fora da mente das pessoas que a usam.
Porém, a escola de pensamento pitagórica da Grécia antiga tinha uma visão diferente. Seus proponentes acreditavam que a realidade é fundamentalmente matemática.
Como argumento em um novo estudo, a matemática é um componente essencial da natureza que dá estrutura ao mundo físico.
Abelhas e hexágonos
As abelhas nas colmeias produzem favos hexagonais. Por quê?
De acordo com a ‘conjectura do favo de mel’ na matemática, os hexágonos são a forma mais eficiente para alinhar o plano. Se você deseja cobrir totalmente uma superfície usando ladrilhos de formato e tamanho uniformes, enquanto mantém o comprimento total do perímetro no mínimo, hexágonos são a forma ideal a ser usada.
Charles Darwin concluiu que as abelhas evoluíram para usar essa forma porque ela produz as maiores células para armazenar mel para a menor entrada de energia para a produção de cera.
A conjectura do favo de mel foi proposta pela primeira vez na antiguidade, mas só foi provada em 1999 pelo matemático Thomas Hales.
Cigarras e números primos
Aqui está outro exemplo. Existem duas subespécies das chamadas cigarras periódicas norte-americanas que vivem a maior parte de suas vidas no solo. Então, a cada 13 ou 17 anos (dependendo da subespécie), as cigarras surgem em grandes enxames por um período de cerca de duas semanas.
Por que são 13 e 17 anos? Por que não 12 e 14? Ou 16 e 18?
Uma explicação apela para o fato de que 13 e 17 são números primos.
Imagine que as cigarras têm uma variedade de predadores que também passam a maior parte de suas vidas no solo. As cigarras precisam sair do solo quando seus predadores estão adormecidos.
Suponha que existam predadores com ciclos de vida de 2, 3, 4, 5, 6, 7, 8 e 9 anos. Qual é a melhor maneira de evitar todos eles?
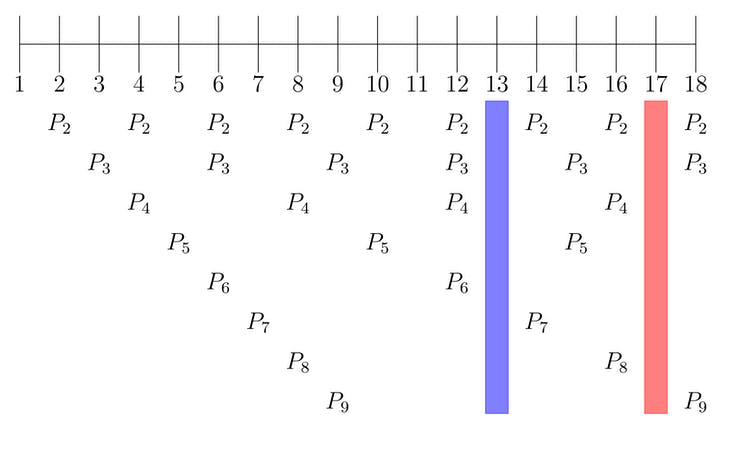
Bem, compare um ciclo de vida de 13 anos e um ciclo de vida de 12 anos. Quando uma cigarra com um ciclo de vida de 12 anos sai da terra, os predadores de 2, 3 e 4 anos também estarão fora da terra, porque 2, 3 e 4 se dividem igualmente em 12.
Quando uma cigarra com um ciclo de vida de 13 anos sai do solo, nenhum de seus predadores sairá do solo, porque nenhum de 2, 3, 4, 5, 6, 7, 8 ou 9 se divide igualmente em 13. O mesmo é válido para 17.
Parece que essas cigarras evoluíram para explorar fatos básicos sobre os números.
Criação ou descoberta?
Assim que começarmos a procurar, será fácil encontrar outros exemplos. Desde a forma de filmes de sabão ao design de engrenagens em motores, até a localização e o tamanho das lacunas nos anéis de Saturno, a matemática está em toda parte.
Se a matemática explica tantas coisas que vemos ao nosso redor, então é improvável que a matemática seja algo que criamos. A alternativa é que os fatos matemáticos sejam descobertos: não apenas por humanos, mas por insetos, bolhas de sabão, motores de combustão e planetas.
O que Platão pensava?
Mas se estamos descobrindo algo, o que é?
O antigo filósofo grego Platão tinha uma resposta. Ele achava que a matemática descreve objetos que realmente existem.
Para Platão, esses objetos incluíam números e formas geométricas. Hoje, podemos adicionar objetos matemáticos mais complicados, como grupos, categorias, funções, campos e anéis à lista.
Platão também defendia que os objetos matemáticos existem fora do espaço e do tempo. Mas tal visão apenas aprofunda o mistério de como a matemática explica qualquer coisa.
A explicação envolve mostrar como uma coisa no mundo depende da outra. Se os objetos matemáticos existem em um reino separado do mundo em que vivemos, eles não parecem capazes de se relacionar com nada físico.
Entrando no pitagorismo
Os antigos pitagóricos concordavam com Platão que a matemática descreve um mundo de objetos. Mas, ao contrário de Platão, eles não achavam que os objetos matemáticos existiam além do espaço e do tempo.
Em vez disso, eles acreditavam que a realidade física é feita de objetos matemáticos da mesma forma que a matéria é feita de átomos.
Se a realidade é feita de objetos matemáticos, é fácil ver como a matemática pode desempenhar um papel na explicação do mundo ao nosso redor.
Na última década, dois físicos montaram defesas significativas da posição pitagórica: o cosmologista sueco-americano Max Tegmark e a física e filósofa australiana Jane McDonnell.
Tegmark argumenta que a realidade é apenas um grande objeto matemático. Se isso parece estranho, pense na ideia de que a realidade é uma simulação. Uma simulação é um programa de computador, que é uma espécie de objeto matemático.
A visão de McDonnell é mais radical. Ela pensa que a realidade é feita de objetos matemáticos e mentes. A matemática é como o Universo, que é consciente, passa a se conhecer.
Defendo uma visão diferente: o mundo tem duas partes, matemática e matéria. A matemática dá forma à matéria e a matéria dá substância à matemática.
Os objetos matemáticos fornecem uma estrutura para o mundo físico.
O futuro da matemática
Faz sentido que o pitagorismo esteja sendo redescoberto na física.
No século passado, a física tornou-se cada vez mais matemática, voltando-se para campos de investigação aparentemente abstratos, como a teoria dos grupos e a geometria diferencial, em um esforço para explicar o mundo físico.
À medida que a fronteira entre a física e a matemática se confunde, fica mais difícil dizer quais partes do mundo são físicas e quais são matemáticas.
Mas é estranho que o pitagorismo tenha sido negligenciado pelos filósofos por tanto tempo.
Eu acredito que isso está prestes a mudar. Chegou a hora de uma revolução pitagórica, que promete alterar radicalmente nossa compreensão da realidade.



